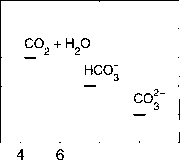[boh4
图1.2.9:PA = 2300 /¿mol kg"1, D1C = 2000 /imol kg"1, Tc = 25°C, 5 = 35时,不同物种对PA(大多数实际用途的碱度)的贡献。通常只考虑总碱度的这个子集就足够了。
在许多海水中,除碳酸外,对总碱度有贡献的最重要的酸碱体系是硼酸和水本身。硼酸盐的碱度和水的碱度是:
硼酸盐碱性= [B(OH)J]水碱性= [OH"] - [H+]。加上这些对碳酸盐碱度的贡献,我们有:
PA = [HCOg] + 2[CO§"]+ [B(OH)"] + [oh "] - [h +]。(1.2.31)
在许多情况下,这与海水jjH的总碱度是一个很好的近似值,我们用PA(最实用的碱度)表示它。本书中给出的绝大多数计算都将使用这种近似。各种化合物对PA的典型贡献是
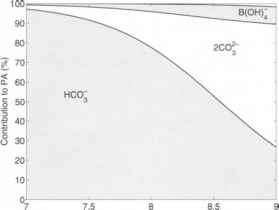
图1.2.10:不同化合物对PA的相对贡献随pH值的变化(DIC = 2000 /(mol kg”)。T,: = 25°c, 5 = 35)。区域表示每种化合物的百分比HCOr(下阴影区域和左垂直轴),2('<)'(白色大区域),B(OH)^~(上阴影区域)和OH-(上白色小区域)。
图1.2.10:不同化合物对PA的相对贡献随pH值的变化(DIC = 2000 /(mol kg”)。T,: = 25°c, 5 = 35)。区域表示每种化合物的百分比HCOr(下阴影区域和左垂直轴),2('<)'(白色大区域),B(OH)^~(上阴影区域)和OH-(上白色小区域)。
如图1.2.9。在我们的例子中,碳酸盐碱度对PA的贡献为96%,表明碳酸盐碱度是到目前为止PA最重要的部分。这种说法也适用于广泛的pE(图1.2.10)。
质子受体和供体
将进一步的酸碱体系(如硼酸和水的解离)纳入碱度的必要性表明,需要一个更一般的碱度概念。事实证明,考虑质子受体和质子供体之间的平衡是一个非常有用的方法,最终将被包括在总碱度的定义中(章节1.2.3)。例如,碳酸盐离子和碳酸氢盐是充当碱的质子受体。另一方面,H+是充当酸的质子供体(回想一下,符号H+实际上代表II30+等物种)。因此,我们可以声明由Fq定义的碱度。(1.2.31)是海水中碱(质子受体)多于酸(质子供体)。其中质子受体是[HCO3], [CO3”]。[BfOH)^]和[OH"],质子供体为II+ (cf. r.a kstraw。1949)。PA等于零的点定义了以下质子条件:
[h +] = [iico3 -] + 2[com + [b (oh)7] + [oh ~]。(1.2.32)质子供体质子受体
这个表达式类似于Fq中定义的质子条件。(1.2.30)为“简化海水”。
介绍了碱度、质子受体和供体以及质子条件的基本概念之后,我们现在开始讨论总碱度的定义。定义总碱度的任务本质上是如何正确展开方程。(1.2.31)和(1.2.32),以便包括进一步的酸碱体系(Dickson, 1981)。
1.2.3 Dickson对碱度的定义
目前最精确的滴定或总碱度的定义是由Dickson (DOE, 1994;Dickson, 1981):“天然水的总碱度因此被定义为相当于质子受体(由解离常数a”< 10~4’5的弱酸形成的碱,在25°C和0时)的过量氢离子的摩尔数离子强度)超过质子供体(含K > 10-4 5的酸)。10对于在海水中发现的化合物,根据迪克森的定义,总碱度的表达式如下:
Ta = [hc03] + 2[c02 -] + [b (0h)-] + [0h -]
+[HPOM + 2[P03"] +[H3Si04] (1.2.33)
+ (NH3) + (HS -] [H +] p - [HS04 -) -(高频)[H3P04]
其中[H+]F为氢离子的自由浓度(比较第1.3节)。Bradshaw和Brewer (1988a)讨论了未知原水解物对总碱度的可能贡献。
定义等当点的适当质子条件为:
f [H +] + [HS04 -] +[高频]+ [H3P04] = [HCOJ] + 2 [C0g "] + [B (0 H) 4] + [0 H -] (1.2.34)
+ [HP02"] + 2[P0M + [H3Si04-] + [HS-] + [NH3],其中质子供体出现在左侧,质子受体出现在右侧。
10值得注意的是,在这种情况下使用的热力学常数K,而不是通常用于海水的化学计量常数K*。原因是K与盐度无关。因此,对弱酸的解离常数的约束是明确的。
根据式(1.2.33),确定样品的总碱度如下:样品用强酸滴定,通常是HC1, pll记录为加酸量的函数。然后利用所有滴定点将理论滴定曲线根据式(1.2.33)与实际数据进行非线性曲线拟合,计算TA。这个过程也被称为逆计算(例如Dickson. 1981;约翰逊和韦德伯格,1982年;Anderson等人。1999)。重要的是,这种TA的测定使用了发生在海水中的酸碱反应的显式模型。碱度的现代定义在概念上不同于第1.2.2节中介绍的操作定义。这是。 the right-hand side of Eq. (1.2.33) explicitly states which acid-base reactions contribute to TA, whereas an operational definition simply provides a, numerical value for TA based on the analytical procedure.
Dickson的定义提出,由pK > 4.5的弱酸形成的碱(如HC03)被认为是质子受体,而pK < 4.5的酸(如H3P04)被认为是质子供体。这个定义明确地将质子受体与质子供体分开。图1.2.11用垂直虚线表示了式(1.2.33)中酸碱体系在/d I = 4.5处的这种分离。有了这个定义,将其他酸碱体系纳入TA的定义就很简单了。请注意,定义质子受体和供体的值4.5的选择是任意的,尽管经过了深思熟虑(Dickson, 1981)。
不带电物种的贡献
令人惊讶的是,式(1.2.33)中也含有不带电的物质,如NH3。高频。H3PO,。值得注意的是,式(1.2..33)因此不能从电荷平衡中推导出来,因为这只涉及带电种。电荷平衡和碱度之间的关系在1.2.4节中详细讨论。我们将在这里简要地解释为什么不带电的物种出现在TA的定义中,使用磷酸举个例子。
质子条件(1.2.34)是氢离子的质量平衡,它定义了所谓的零质子水平。(当然,这并不意味着溶液中没有质子!)对于特定的酸碱体系,质子条件定义了哪些物种被认为是质子供体和受体。图1.2.12说明了磷酸的情况。在这种情况下。H2POj定义了零能级的质子
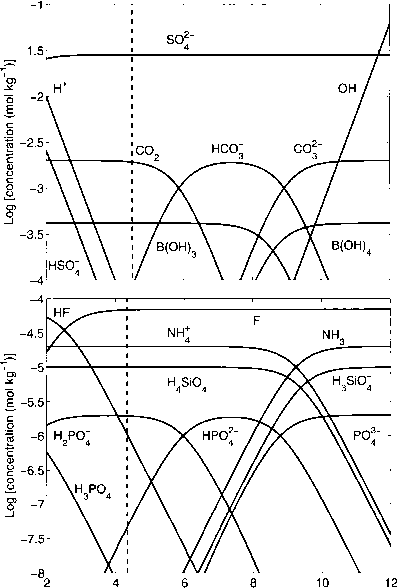
图1.2.11:扩展Bjerrum情节显示了海水中与TA相关的酸碱体系。pH = 4.5处的垂直虚线表示哪些物种被认为是质子供体和受体(参见图1.2.12)。
图1.2.11:Bjerrum扩展图,显示海水中与TA相关的酸碱系统。pH = 4.5处的垂直虚线表示哪些物种被认为是质子供体和受体(参见图1.2.12)。
因为在pR = 4.5.11时H3P04为优势种
11在一些文献中出现了一个明显的混淆,即零水平
-
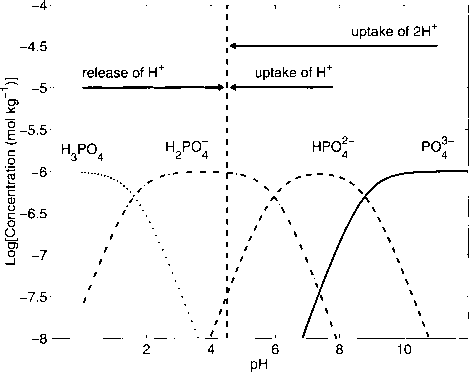
- 图1.2.12:TA定义在磷酸体系中的应用。IrEPO^定义了质子的零能级。因此,P04~是一个比H2PO7少两个质子的质子受体。H3PO4是比H2PO-多一个质子的质子供体。
质子供体,在转化为II2P04时提供质子。这就是为什么总碱度的定义中也出现了不带电的物质。
对于碳酸,HCO3和CO3-被认为是质子受体,因为这两种物质都吸收质子形成H-^CO^。在pli = 4.5处,定义零质子水平的主要化学物质是碳酸(II2CO:5和C02 + H20),我们可以说HCO3,例如,含有比定义的零质子水平H2C03更少的质子(图1.2.13)。一般来说,式(1.2.34)的右侧由质子含量低于定义的零水平的物种组成,而磷酸则选择了H3PO4。这并不是错误的,只是令人困惑,因为这意味着添加H3PO4不会改变总碱度——尽管你可以将溶液酸化到足以将碳酸盐碱度降低到零(Dickson,个人交流)。
-
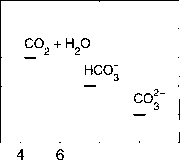
- 8 10 12

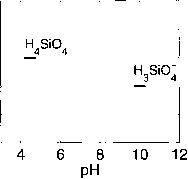
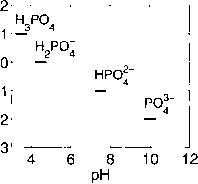
图1.2.13:几种酸碱体系的化学种类及其质子能级;在给定的pH值范围内,优势物种被指出。特定酸碱体系的零级质子由pH = 4.5时的优势种来定义。对于碳酸,硼酸,硅酸和磷酸,这些物种是H2CO3, B(OH)3, hiisioi和H2P04”。H2O(未显示)是包括H2O, H+和OH-的整个pH范围内的优势物种,pH范围从低于4到高于10,因此定义了水解离的零质子水平。
式(1.2.34)的左边由质子多于定义的零水平的那些物种组成(Dickson, 1981)。
总结。介绍了碱度的概念,从碳酸盐碱度(CA)开始。总结一下关于碱度的初步讨论,我们可以说:“碱度与弱酸离子的电荷有关,可以用滴定法测定。”进一步的酸碱反应发生在天然海水中,即硼酸盐和水的碱度被添加到生成PA(碱度是最实际的用途)。最后,由式(1.2.33)给出了基于质子受体和供体平衡的总碱度(TA)的正式定义。此外,还概述了测量TA的方法(详见Dickson, 1981;
约翰逊和韦德伯格,1982年;Anderson等人。1999)。要计算的清算碳酸盐系统使用测量的TA作为主变量的参数见附录b。到目前为止所讨论的主题对海洋中二氧化碳的测量至关重要。以上就是我们从化学角度对碱度的处理。
本章的其余部分不会对总碱度的定义增加任何新内容。正式的定义通常可以满足总碱度概念的应用,但通常需要更深入的理解才能回答以下问题:碱度的变化是否由于氮同化如果是藻类,它是如何变化的?答案是肯定的,尽管NOJ和111没有出现在TA的正式定义中,见下文。雷竞技csgo
1.2.4总碱度和电荷平衡
前面几节从化学的角度讨论了总碱度,现在我们将从物理或地球化学的角度探讨碱度的概念。它将表明碱度与海水中的电荷平衡密切相关,这使得它成为一个吸引人的概念,因为可以推导出诸如总碱度守恒等性质。
silen(1961)认为,考虑到海洋的起源,我们可以说海洋是一个巨大的酸碱滴定的结果,其中酸如IlCl。从地球内部泄漏出来的II2S()4和co2用原生岩石风化产生的碱进行滴定正如我们在前几章中所看到的,海水的缓冲能力和碱性性质主要归因于溶解碳酸盐物种。因此,人们可能会说,海洋的缓冲特性是由于碳酸的存在,这在某些方面是正确的。
silen(1967)指出。然而,与随着时间的推移通过海洋系统的酸和碱的数量相比,溶液中碳酸盐的缓冲能力少得可怜。关于从酸碱平衡的角度来定义总碱度,这种观点提出了海水碱性的一个更根本的原因。我们将看到,海洋中碱度的起源与海水中主要保守离子的电荷平衡有关。
西伦继续说:“在酸碱滴定法中,火山与风化作用的对比,我们似乎离等当点只有0.5%左右。顺便说一句,这比大多数化学学生第一次滴定时做的要好。”
主要阳离子Na+, K+, Mg2+和Ca2+的电荷总和并不完全由主要阴离子CI-和SO^-平衡。这种微小的电荷不平衡导致了海洋中的总碱度,主要由碳酸的阴离子来补偿。我们可以说:
总碱度等于保守的阳离子和阴离子之间的电荷差
简单体系中的总碱度
总碱度与电荷平衡之间的密切关系将首先通过考虑比天然海水简单的水溶液来证明。海水是一个非常复杂的体系,因为它含有许多不同的阳离子和阴离子以及一些弱酸和弱碱。McClendon et al.(1917)指出:
“大海的构成太复杂了,不可能有任何简单的数学关系”
(cf. Dickson, 1992)。为了消除与天然海水相关的一些并发症,首先讨论了仅含有Cl~, Na+和一种弱酸的简单体系。
体系I: Na+, CI-和一个弱酸
让我们考虑一个只含有Na+, CI-和一种单质子弱酸的溶液,用HA表示:
pKA = 6。规定了以下初始条件:
[Na+]j = 0.6 mol kg-1, A总浓度AT = [A-];+ [HA]•= 2300 /¿mol kg-1;因此pH值与典型的表层海洋条件相似,钠的浓度与S = 35时海水中所有阳离子的总电荷量相似,A的总浓度与表层海水中典型碱度值数值相似。
根据规定的值,可以计算出OH-和a的初始浓度:
哦-,= tfw / tH + k = 9.6 / /摩尔公斤(”),- = / (1 + 8 [H +] / / v), = 2286 / /摩尔公斤
值得注意的是,CI的浓度没有规定。设定好了。然而,通过要求电中性:
[Cl ~] = [Na +] + [H +] -["] -[哦-)= 0.5977摩尔公斤”1。
因此,O-的浓度略小于Na+的浓度。强碱和强酸的正离子和阴离子浓度之差,即保守离子的电荷不平衡为:
[Na+] - [CP] = TA = [A-] + [OH"] - [H+]。(1.2.35)
式(1.2.35)的右边类似于式(1.2.33)中酸碱反应对TA的定义。然而,我们现在已经完全用保守离子来表示碱度,即式(1.2.35)的左边。正是这个性质使TA成为保守量。式(1.2.35)左侧的表达式表示为“显保守碱度”或
因为每一项,不仅整个表达式是保守的;式(1.2..35)右侧的表达式用符号TA表示。我们将看到,在确定生物地球化学过程引起的TA变化时,考虑TA'ec'是非常有用的(第1.2.7节)。
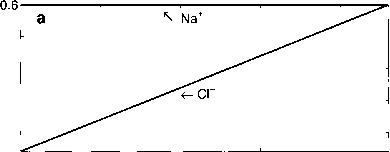
对于简单体系,保守离子的电荷平衡与TA的关系可以通过考虑HC1对体系的滴定来说明(图1.2.14)。图1.2.14a中标注了“C”,图1.2.14b中包含了质子受体和供体TA。初始时,[Cl~]与[Na+]相比有少量的亏损,约2.3 inmol kg-1,恰好等于初始的总碱度(图1.2.14a)。在滴定终点,最初的赤字已被补充的HC1。此时pH为4.32,氯离子和钠离子浓度相等,总碱度为零。
[Cl~] = [Na+]对应质子零能级的点,即酸碱体系的等当点:
如图1.2.14b中的圆圈所示。此时,A-几乎完全被II+中和,转化为HA。这里所考虑的简单体系的总碱度,同样可以通过质子受体超过质子供体(TA)或保守离子的电荷差来很好地定义
从图1.2.14可以看出,考虑保守离子比处理酸碱体系的所有细节要简单得多。
0.5995
0.5995
0.5985 -
0.5985 -
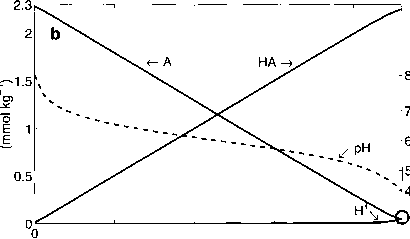
图1.2.14盐酸滴定体系I, (a)保守离子浓度,(b)酸碱体系化合物浓度和ph值,差值[Na+] - [CI-]正好等于总碱度,TA = [a ~] + [OH -
图1.2.14盐酸滴定体系I, (a)保守离子浓度,(b)酸碱体系化合物浓度和ph值,差值[Na+] - [CI-]正好等于总碱度,TA = [a ~] + [OH -
体系二:食盐和溶于水的弱酸
如上所述,系统I的总碱度与地表海水中观测到的典型值相似。结果表明,碱度是由于保守离子的电荷不平衡造成的。为了强调这个小的不平衡的重要性,我们现在将考虑一个不平衡缺失的系统。体系II由含有体系i中讨论的弱酸2300¿i/mol kg-1的水溶液和0.6 mol kg-1的Na+和CI-组成。换句话说,体系II是由加入弱酸和食盐(NaCl)的纯水组成的。体系II与体系i非常相似,但重要的区别是体系II中Na+和Cl~的浓度是相同的。与系统I相比,系统II的pll不是一个独立的初始参数,而是可以通过电中性计算:
0 = TA = [Na+] - [CI"] = [A-] + [OH"] - [H+]
得到的[H+]三次方程的数值解得到pH ~ 1.32。因此,将弱酸添加到pH = 7的中性食盐溶液中会导致低pll值。在体系I中,只有在加入相当数量的强酸后,才能达到这个值。实际上,系统1滴定到质子pH值的过程把系统I变成了系统IT。因此,在滴定至总碱度为零的等当点后,体系II的pll等于体系1的pH也就不足为奇了(见图1.2.14)。在体系II中,大多数弱酸以不带电的形式存在,即pll < pK,因此该体系无法缓冲任何酸的加入。
通过对体系1和体系2的比较,得出了保守离子电荷的不平衡是造成碱度的原因。因此,系统是缓冲的。在海水中,TA随盐度变化,见1.2.7节。这种变化是由于保守离子的总电荷不平衡随盐度而变化。(请注意,海盐的成分几乎是恒定的)。因此,海水的缓冲能力是由于保守离子的电荷不平衡。淡水系统通常只含有少量的保守离子,因此只有弱缓冲。例如,由于植物吸收二氧化碳或输入酸雨,酸浓度的微小变化会导致pH值的大变化。
1.2.5天然海水中的电荷平衡
天然海水含有的离子比上面讨论的简单体系多得多。然而,同样的电中性原理也适用于海水。海水中所有离子的电荷之和必须等于零。这在数学上表示为:
650 600 550 500
1 |
450 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
O) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
^ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
O |
One hundred. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
E |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
E, |
80 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
60 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
40 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
20. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
图1.2.15:海水中主要离子的电荷平衡(cf. Broecker and Peng, 1998)。保守阳离子对阴离子的少量过量电荷主要由 阳离子阴离子 [Na+] + 2[Mg2+] + 2[Ca2+] + [K+] +…+ (H +) F - (CI) - 2 [S02 "] -[三]- [HCO3] 2 [C0§~]- [B (OH) 4][哦"]-…= 0 (1.2.37) I中[c•]和z-分别为化合物j的浓度和电荷。 的收费余额海水中的主要离子图1.2.15所示,其中所有次要物种均被忽略。首先,这表明保守正离子和阴离子之间的电荷不平衡相对于它们的总浓度(~ 2 vs. ~ 600 mmol kg-1)非常小。我们还看到了少量的过量正电荷
([Na+] + 2[Mg2+] + 2[Ca2+] + [K+]) /负电荷([CI”]+ 2[SO^-])由[HCO3] + 2[C02”]+ [B(OH)~]补偿,其中后者是对TA最重要的贡献。表1.2.7列出了S = 35时海水中主要保守阳离子和阴离子的浓度和电荷浓度。保守阳离子的总电荷浓度为605.0 mmol kg-1,而保守阴离子的总电荷浓度为602.8 mmol kg-1。2.2 mmol kg-1的微小电荷不平衡等于海水中的总碱度(严格来说,只有忽略磷酸盐、氨和硫酸氢盐离子时才正确,参见附录C.l)。 碱度可以用保守离子的电荷不平衡来表示,这一事实使我们可以推导出一个非常有用的方程。式(1.2.37)可以改写为:左侧为所有保守离子,右侧为所有非保守离子: Y^保守阳离子- J2保守阴离子 = (HCO3) + 2 [co2] + [B (OH) 4 -] +[哦——]- [H +] (1.2.39) ±次要化合物 这个表达式非常类似于式(1.2.31)中给出的PA(最实际的碱度)。忽略“minor compounds”这个词,我们可以这样写:
式(1.2.40)的右边简单地用质子受体和供体表示PA,如本章第一部分所讨论的那样。然而,式(1.2.40)的左边完全用保守离子(明确的保守碱度)表示PA,这是非常有用的,将在下面详细说明。 1.2.6总碱度守恒总碱度可以用海水中保守离子的电荷平衡来表示,这一事实使我们可以在不使用总碱度的正式定义(式1.2.33)的情况下作出重要的推论 首先,如果海水样品的总碱度以mol kg-1为单位表示,则总碱度在温度和压力变化过程中保持完全守恒。这直接来自TA'e€),因为1千克海水中保守离子的浓度不受温度和压力变化的影响。从以弱酸为单位的碱度表达式(式(1.2.40)的右侧)来看,这并不明显,因为在这个表达式中,化学物种的单个浓度确实随温度和压力而变化。这是因为化学平衡(pA " s)取决于温度和压力。 其次,保守离子的电荷不会改变,例如,当二氧化碳在水和空气之间交换或当二氧化碳被藻类吸收或呼吸时。在吸收和释放二氧化碳的过程中,式(1.2.40)右侧的单个浓度可能会因为二氧化碳镑和ph值的变化而发生巨大变化。 是恒定的 13请注意,式(1.2.40)中电荷平衡和碱度之间的关系在这里严格地只导出了PA,而不是TA。TA的推导可在附录C.l中找到。 因为保守离子不受影响,所以碱度是恒定的。另一方面,如果在样品中加入强碱,如NaOH,碱度会增加,因为[Na+],因此TA'ec'也会增加。如果向样品中加入强酸,如HC1,碱度会降低,因为[CI-] (TA'ec'表达式中带有负号)增加。注意,每加入一个单位的强碱或强酸,TA变化一个单位,因为这些物质完全解离。类似地,海洋中生物地球化学过程引起的TA变化也可以理解(章节1.2.7)。 质量、盐、溶解无机碳和总碱度的混合和守恒。 当两种不同性质的海水(i = 1,2)混合时,质量(A/-),盐(M(- 5¿),溶解无机碳(Mi■i) i('()。总碱度(Mt■TA。J,分别加起来得到混合物的确切性质值(指数m): Mm = M, + M2 (1.2.41) 嗯- sm =•!/,•-v,••s, (1.2.42) ■DIC, + M2•DIC2 (1.2.43) Mm-TAm = 1/, TA,•\/,-T\, (1.2.44) 因此S^ I) IC(。和TA(以重量(每质量)为单位。相反,当两个水体混合时,DIC或TA的体积和单个组分如[C02]、[HCO3]或[CO2-]都不守恒(见练习1.9和1.10)。DIC和TA的守恒特性是在海洋碳循环模型中使用这两个量作为预测变量的原因。 第三,混合过程中总碱度保持不变。当两个性质不同的水团混合时(盐度温度71-,质量M¿,i = 1,2),保守离子的电荷是相加的,即遵循以下关系(参见关于混合的方框): ■5>2vJ, (1.2.45) 在这里求和指数S覆盖了所有保守离子;指数rri表示混合后的量,Mm = M1 + M2-因此,总碱度也是加性的,与之相关 Mm-TAm = M1-TA1 + M2。TA2  图1.2.16:印度洋表层水域(WOCE Section I07N, F. Millero和K. Johnson,http://cdiac.esd.ornl.gov/oceans/CDIACmap.html).在这种情况下,总碱度与盐度线性相关。 图1.2.16:印度洋表层水域(WOCE Section I07N, F. Millero和K. Johnson,http://cdiac.esd.ornl.gov/oceans/CDIACmap.html).在这种情况下,总碱度与盐度线性相关。 成立。换句话说,总碱度是一个守恒量,就像质量、盐或溶解的无机碳一样。 1.2.7海洋总碱度 导致总碱度变化的过程有几个首先,保守阳离子和阴离子之间的电荷差随盐度的不同而不同。因此,海洋中的TA与盐度密切相关(图1.2.16)。盐度的变化是由于降水、蒸发、淡水输入以及海冰的形成或融化,并引起总碱度的相应变化。 海洋总碱度的第二个主要变化是由于海洋生物产生碳酸钙(CaC03)的生物沉淀 斯托尔(Stoll, 1994)对这一主题也有总结。 如球石虫、有孔虫、翼足类和珊瑚,以及溶解钙质壳或骨骼。降水导致Ga2+浓度降低。因此,保守阳离子和阴离子之间的电荷差减小,总碱度也减小。沉淀1 mol CaC03使DIG减少1 mol, TA减少2 mol。请注意,这些变化与生物钙化所使用的碳源(HGOg, C03~,甚至C02)无关。因此,不能通过观测海水中DIG和TA的变化来推断碳源。 海洋总碱度的微小变化与植物对氮的同化和有机物在再矿化过程中溶解无机氮的释放有关。Brewer和Goldman(1976)和Goldman和Brewer(1980)研究了植物同化硝酸盐、氨或尿素引起的碱度变化。他们发现,碱度的变化与一个简单的化学计量模型是一致的,在这个模型中,NO3的吸收由OH~的产生来平衡(即碱度增加),Nllj”的吸收由H+的产生来平衡(即碱度降低);尿素被同化时碱度不发生变化。 TA'ec'表达式可以用来概括由于某些生物地球化学过程引起的碱度变化。这种方法非常方便,因为TA'ec'(保守离子)的每一个组分都可以变化,而不影响该表达式中的任何其他组分。另一方面,碱度弱酸(质子受体和供体)表达的单一成分的变化通过EC02和ph的变化影响所有其他成分。基于TA 1.沉淀一摩尔CaC03:碱度降低两摩尔(项:2[Ga2+])。 2.溶解一摩尔CaC03:碱度增加两摩尔(术语:2[Ca2+])。 3.藻类对DIG的吸收假设是通过平行吸收H+或释放OH~来保证藻类的电中性:碱度无变化。 4.藻类吸收一摩尔硝酸盐(NO3)的假设是通过同时吸收H+或释放油来保证藻类的电中性”:碱度增加一摩尔(术语:- [NO3])。这与在不同氮源上生长藻类的实验室实验是一致的(Brewer和Goldman (1976);Goldman and Brewer(1980))。 5.藻类物质的再矿化对碱度有相反的影响。 测定由于藻类摄取而引起的碱度变化氨、磷酸,等需要定义一个对应于Dickson给出的完整的TA右手边的TA左手边(Eq.(1.2.33))。这可以在附录C.l中找到。 总结。总碱度定义为1千克样品中质子受体多于质子供体的氢的摩尔数。在实际应用中,海水总碱度可定义为PA = [HCO"]+2[C02~]+[B(0H);]+[0H-]-[H+]。由TA等于保守正离子和阴离子的电荷差,可知TA是一个保守量。当二氧化碳与大气交换或被植物吸收或释放时,总碱度不会改变。但总碱度随盐度(沉淀、蒸发)、碳酸钙沉淀和溶解以及溶解无机氮的同化和释放而变化。 进一步阅读:Dickson (1992), Bradshaw和Brewer (1988b), Anderson等人(1999)。 在实验室实验中,生物学家经常添加比在海洋中观察到的浓度高得多的营养物质。这会导致碱度的变化吗?如果是,当你向天然海水样品中添加营养物质以匹配f/2介质的浓度时,碱度会发生多大变化?f-培养基含有882 /jmol kg-1硝酸盐,36 ftmol kg-1磷酸盐和30 /imol kg-1硅酸盐(Guillard和Ryther, 1962)。f/2-medium的含量只有它的一半。天然海水样品应已含有15 /imol kg-1硝酸盐、1 /imol kg-1磷酸盐和15 /imol kg-1硅酸盐。营养物以NaN03、Na2HP04和Na2Si03的形式加入。 考虑在Tc = 25°C和S = 35的封闭瓶中培养非钙化藻类。初始条件为DIC = 2 mmol kg-1, TA = 2.3 mmol kg"1, NO" = 20 /tmol kg"1。一段时间后,藻类吸收了碳,并吸收了所有的硝酸盐。假设雷德菲尔德比率C:N = 106:15,计算[CO2]的变化。这种变化有多少是由于碱度的变化? 当二氧化碳从海水中吸收或流失时,总碱度保持不变。碳酸盐的碱度发生了什么变化? 考虑两个质量相同(1000千克)、温度相同(25°C)但盐度不同(Si = 30, S2 = 40)的海水。计算在地表压力下混合前后水体的相应体积。体积守恒吗?提示:海水密度作为盐度、温度和压力的函数(p(S,T, p))在附录a .13中给出(参见Millero和Poisson, 1981;吉尔,1982)。一个包含p(S)的MATLAB例程。T.P)可在我们的网页上找到;“http://www.awi-bremerhaven.de/Garbon/co2book.html”。 考虑两个质量相同(1千克)、温度相同(25°C)、盐度不同(Si = 30, S2 = 40)、溶解的无机碳(DICi = 1800 //rnol kg"1, DIC2 = 2000 funol kg"1)和总碱度(TAi = 2100¿tmol kg"1, TA2 = 2300 /zmol kg^1)的海水。计算在地表压力下混合后,干旱前水体中CO2、HCO”和CO2”的相应浓度。CO2总量、HCOJ和CO2“守恒”吗? 1.3 pH值范围 “pH值范围……在海水中是海洋化学中比较混乱的领域之一。” “对于许多人来说,选择一个合适的pH值刻度来测量海洋pH值仍然是一个困惑和神秘的话题……” 本节的目标是介绍化学海洋学中使用的不同pll标度,并简要讨论这些标度的起源。这需要一点工作,但它将表明,海水pH值刻度没有什么神秘的。基于简单的相互转换,将估计不同尺度之间的数值差异。最后,我们将通过一个例子说明,如果忽略pll尺度之间的差异,在计算pC02时可能出现的错误。 在下面,我们将讨论两个主要问题:为什么以及什么时候我们应该关心不同的pH值范围(定义)? 为什么?的平衡常数如H2C03的第一和第二酸度常数必须与pH刻度一致(见Dickson (1984;详情1993a)。如果在碳酸盐岩体系的计算中忽略这一点,就会出现严重的错误(参见第1.1.6节)。 什么时候?海水中不同的p\I尺度值最多相差0.12个单位(见公式)。(1.3.57),(1.3.58))对应于pK*和pl(2(见式(1.3.60))的可比性差异。因为这些差异远远大于pH测量的期望精度,当pH是一个主变量时,我们应该关心不同的pH尺度。请注意,不同出版物的酸度常数之间的差异可能主要是由于使用了不同的pH值尺度。 在高中,我们学过pH (latat。为氢离子浓度的负公对数(pondus hydrogenii): 这个定义可以追溯到S0rensen(1909)。事情有点复杂,原因如下: •“可以肯定地说自由质子”(氢离子)"在水溶液中不存在大量的"相反,质子与水分子结合,形成了H30+离子;反过来,它又与其他三个水分子氢键成键,形成一个氢氧化氢离子。”(迪克森,1984,第2299页);也比较马克思等人(1999)和海因斯(1999)。因此,符号“H+”代表水合物配合物,而不是自由氢离子的浓度。如1.1节所述,将[H+]称为氢离子浓度比较方便。 •在一个精炼的理论中,我们应该使用活动(一个“有效的”集中;用a)代替浓度 ph高中:= - log[H +]。 PHa = " loS aH+•。 不幸的是,无法根据式(1.3.48)测量pH值。其原因是,单个离子的活性不能通过实验确定,因为需要电中性,单个离子的浓度不能独立变化(例如,Klotz和Rosenberg, 2000)。 国际纯粹与应用化学联合会(IUPAC)给出了NBS15 pH值的操作定义。NBS pll量表由一系列标准缓冲溶液定义,其指定pH值接近- logaH+的最佳估计值,即pHNBS接近但不等于/'lla pHa和pHNBS的参考状态为无限稀溶液,即当[II+]在纯水中趋于零时,1I+, 7B+的活度系数趋于一。 NBS标准缓冲溶液的离子强度很低,约为0.1。相比之下,海水的离子强度较高,约为0.7。因此,不建议在海水中使用电极进行锁相环测量时使用NBS缓冲液,因为缓冲液和海水之间离子强度的巨大差异会导致校准和样品测量之间的液体结电位发生重大变化16。更糟糕的是,这些变化取决于所使用的电极系统。由于液体结电位的这种变化造成的误差大于0.01 - 0.001 pH单位的期望精度(Wedborg等人,1999)。 哈哈。nsson (1973a)通过采用海水作为标准状态和引入基于人工海水的新的pH标度,极大地改善了这种情况。在这个pH标度(称为“总”标度)上,当[Il +]T在该标度所基于的纯合成海水中趋于零时,活度系数7H+趋于一(关于[H+]T的定义,见下文)。Haiisson (1973a)提出了一套新的基于人工海水的标准缓冲液,并根据这些缓冲液赋予pH值 ljNBS:国家标准局,现为NIST:国家标准与技术研究所。 16液体结电位是电极中的溶液与测量溶液之间的电位差。理想情况下,它只取决于电极溶液和测量溶液的组成,但实际上,它也取决于液体结的实际设计(Wedborg et al., 1999)。 物种z的化学势/¿t与浓度c有关,活度a通过fi, - = RT In a: = RT In (c,y,),其中/x°是参考状态的化学势,■>是活度系数。7, - > - 1在海水中的关系对应于的值的一定选择。 他的新酸碱度量表。这种方法的一个很大的优点是,由于两种溶液的组成非常相似,缓冲液和样品之间的液体结电位的变化大大减小。 除了总比例尺外,还提出了在海水中使用的自由比例尺和海水比例尺,这将在下面讨论。我们用pHF表示自由比例尺,用pHT表示总(或汉森)比例尺,用pHsws表示海水比例尺。它们的定义如下: 公积金= 日志(H +) F (1.3.50) pHT = -log([H+]F + [HS04] ) =日志(H +) T (1.3.51) PÏÏ sws = -log ([H+]F + [HSO4] + [HF]) = -log[H+]sws。 (1.3.52) 其中[H+]F是“自由”氢离子浓度,包括水合形式,见上文。 当然,自由尺度在概念上是最清晰的。然而,很快就会发现,这个概念受到HS04的稳定常数Kg的影响,这不是一个简单的任务,必须在海水中准确确定(Dickson, 1984;1993 b)。在海水中,S04~等离子发生质子化: 因此,在含有硫酸盐离子的海水介质中,总氢离子浓度为: 分析上,只能确定[H+]t (Dickson, 1993b;Wedborg et al., 1999)。因此,[H+]F必须根据 这涉及到Kg。因此,使用自由比例尺需要海水中K%的准确值,而这是很难获得的。 汉森(1973a)使用了含有硫酸盐离子的介质,因此他将总刻度定义为式(1.3.51)所示。这个刻度在其定义中包含了硫酸盐离子的影响,因此绕过了确定A'g的问题。在这个尺度上,当([H+]F + [HSO4])在离子介质中趋于零时,活度系数趋于一。 海水水垢 如果介质中另外含有氟离子,我们还必须考虑F~的质子化: 例如,Goyet和Poisson(1989)就使用了这种介质。那么总氢离子浓度为: [H+]k + [HS04-] + [HF],从而得到海水尺度的定义,式(1.3.52)。因此,总比例尺与海水比例尺之间的差异仅仅源于比例尺所依据的介质是否含有氟离子。然而,这种差异很小,因为海水中IISO4的浓度远大于HF的浓度。 底线如下。已经提出了三种用于海水的pil秤。使用自由比例尺需要准确测定HSO4在海水中的稳定常数,这不是一件简单的事情。总量和海水尺度的定义绕开了这一问题。总规模和海水规模之间的差异可以通过不同研究人员的实验室协议的差异来解释。 1.3.1 pH值的换算 [H +] f 1 + s,:k;1 + sT/iq + ft/k* 或 (1.3.53) 公积金 = PHSWS + log (1 + sT/iq + Ft/K*f) 式中,Kg和lip分别为硫酸氢和氟化氢的稳定常数(见附录A)。 St = [so2 -] + [hso4] ~ [so2 -] (1.3.54) 总硫酸盐浓度是多少 Ft = [F-] + [HF] ~ [F-] (1.3.55) 是氟化物的总浓度。由式(1.3.53)可知,标度转换基本简单。为了在不同尺度之间进行准确的转换,必须准确地知道海水中的稳定常数Kg和A'p。如上所述,这似乎很困难(Dickson, 1993a)。因此,当数值在不同尺度之间进行比较时,计算中引入了不确定性。然而,这种不确定性与简单忽略尺度转换时产生的不确定性相比是很小的。 让我们利用可用的Kg和Kp数据来估计海水中pH值尺度之间的数值差异。数值差异由术语log (1 + ST/和log (1 + ST/Kg + FT/Kp)给出。S = 35海水的ST和FT值可在DOE(1994)中找到: ST = 28.24 mmol (kg-soln)-1 T _i (1.3.56) 当S = 35, Tc = 25℃时,~ 0.10 mol kg-1, Kp ~ 0.003 mol kg-1,得到: 日志(左 + St/IQ) = - 0.11 (1.3.57) log (1 +VA* . log + FT/Kf) = - 0.12 (1.3.58) 换句话说,在标准条件下,自由比例尺上报告的样品pH值比总量比例尺和海水比例尺分别高约0.11和0.12个单位。例如,如果pHF = 8.22,那么pHT = 8.11, pHsws = 8.10。这给我们一种感觉,当忽略比例转换时,计算中可能出现错误。与pH值测量的准确性和精密度相比,这种差异是巨大的。Millero等人(1993b)给出的pH值测量精度为±0.002(有关测量技术的最新进展,参见Dickson (1993b)、Bellerby等人(1995)和Wedborg等人(1999))。表1.3.8总结了目前使用的pR量表及其之间的估计差异。 表1.3.8: pH值的大小和差异 他们之间。 pH值范围 适用的 自由标度'1的参考差 在 状态 pHF - pll2 PHNBS 淡水 纯水 公积金 海水 人工海水 pllr 海水 人工海水 ~ 0.11 P ^慢波睡眠 海水 人工海水 ~ 0.12 这里要学习的最重要的一课是:检查使用的pH值刻度!如果忽视这一点,就会出现很大的不确定性。与这些不确定性相比,由于A£和A'p值的不确定性而导致的实际刻度转换过程(式(1.3.53))所产生的误差很小。如果共同体就单一酸碱度量表达成协议,就可以消除不同的/»I量表之间的转换所产生的潜在问题。一个很有希望的备选方案当然是总规模。 1.3.2酸度常数的换算 Dickson和Millero(1987)描述了不同pH值范围内酸度常数的转换。一个典型的平衡关系如下: [C02-]/[HC0,3] = A.;t/[H+]t (1.3.59) 其中指数“T”表示平衡常数和pH指的是总尺度。现在将总比例尺转换为自由比例尺。取负对数得到: = pK*n + log (1 + 5X/A'g) - php -■pK 2*f =回目* K-pHF。(1.3.60) 当我们改变pll刻度时,式(1.3.60)的左边不会改变,因为碳酸盐离子和碳酸氢盐的浓度是物理量,不能依赖于我们选择的pH刻度。因此,式(1.3.60)的右侧也没有变化。因此,如果我们从总pH值切换到自由pH值,pH值就会更高 图1.3.17:[C02]和pC02随pH的变化(Tc = 25°C, S = 35, DIC = 2 mmol kg-1)。如果忽略pH刻度之间的转换,pH值的误差可能高达0.1个单位,导致计算出的pC02相差约100 /tatm。 图1.3.17:[C02]和pC02随pH的变化(Tc = 25°C, S = 35, DIC = 2 mmol kg-1)。如果忽略pH刻度之间的转换,pH值的误差可能高达0.1个单位,导致计算出的pC02相差约100 /tatm。 这个刻度是0.1个单位,那么pA'2F也必须高0.1个单位。为了说明如果忽略这些差异可能出现的潜在误差,请将C02浓度视为恒定DIC下pH值的函数(图1.3.17)。pH = 8.0, 5 = 35, Tc = 25℃,DIC = 2 mmol kg-1时,pH每增加0.1,[C02]减少约3¿¿mol kg"1。计算出来的pC02的相应差异大约是100 /xatm!这个数字已在第1.1.6节中给出,其中讨论了平衡常数的选择。 在Dickson和Goyet的手册(DOE, 1994)中指出,除硫酸氢盐离子外,所有酸性常数都用“总”(Hansson)氢离子浓度表示(DOE, 1994,第5章,第12页)。这是非常有用的,因为当使用的pH值没有明确说明时,可能会引起混淆。 总而言之,平衡常数的定义与一定的ph比例尺一致。目前,海洋化学家使用的刻度为pHT或pHsws 相差0.01;这两种量表与自由量表(pHF)的差异约为0.1。在海水中测量时不建议使用NBS刻度。继DOE(1994)和Wedborg等人(1999)之后,本书将使用总pH值刻度(除非另有说明)。 进一步阅读:Dickson (1984, 199.3a), Millero等人(1993a), Wedborg等人(1999)。 1.4分压和逸度 可以分析确定的四个碳酸盐体系参数是:co2, TA, pH和pC02碳酸盐化学海水样本。三个变量SC09、TA和p\[已经在前面的章节中讨论过了。这一节讨论二氧化碳的分压。要指出的是,分配给海水样品的二氧化碳分压是指气相中二氧化碳与海水平衡时的分压。一旦确定了pC02,或者更准确地说,逸度/二氧化碳,就可以使用亨利定律计算溶液中溶解的二氧化碳浓度,并将其作为主变量(附录B)。还可以计算海洋和大气中pC02的差异,并使用差异来估计空气-海洋气体的净二氧化碳通量(例如高桥等人,1997年)。 海洋化学家报告说,海洋表面的二氧化碳含量为逸度,这与更广为人知的分压有关。然而,测量的量是二氧化碳的摩尔分数。下面我们将解释这些量之间的差异。 1.4.1摩尔分数和分压 气体a的摩尔分数x是a的摩尔数除以样品中所有组分的摩尔数:xA = nA/D-n;。摩尔分数以摩尔摩尔-1为单位表示;例如,2'C02通常以//mol mol-1表示。对于完美气体,摩尔分数等于体积混合比(每卷体积),单位PPMV (百万分之一体积). 气体a的分压与它的摩尔分数成正比:Pa ~ xa’P-其中P是混合物的总压。这可以作为分压的定义,即使气体行为不完美(Atkins, 1998)。分压单位为大气压(atm)。对于气体的混合物,我们可以写成: Pa + Pb + Pc + - =(®a + %b + xc +•••)P = P 这表明当总压为1atm时,气体的摩尔分数在数值上只等于它的分压。表1.4.9总结了用于描述气相中二氧化碳的各种量。 数量 文学符号 单位 价值” 备注 摩尔分数 , TC02 / /摩尔mol-1 360.0 在干燥空气中 混合比/浓度 xC02 ppmv 360.0 在干燥空气中 分压 二氧化碳分压 / /自动取款机 349.0摄氏度 湿度100% 不安定 fC02 / /自动取款机 347.9 d 湿度100% 数值是指,或从干燥空气中测量的XCO2 = 360 //mol mol 1计算出来的。'也用于摩尔分数,假设混合物中的所有气体都表现完美。 数值是指,或从干燥空气中测量的XCO2 = 360 //mol mol 1计算出来的。'也用于摩尔分数,假设混合物中的所有气体都表现完美。 cAt T = 25°C, S = 35。^当T = 25°C时。 大气中的二氧化碳 当测量大气中气体样品的二氧化碳含量时,通常报告为摩尔分数xC02,或简单地称为二氧化碳浓度。如果数值是根据二氧化碳的分压来报告的,数值会随着高度迅速下降,因为分压取决于总压,而总压是高度的函数。相反,co2的摩尔分数在不同海拔高度可能相当恒定。显然,摩尔分数和分压是完全不同的量,甚至在 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
继续阅读:动力学
这篇文章有用吗?
读者的问题
-
克里斯蒂娜3个月前
- 回复